Silver machine
- Not to be confused with Silver Machines.
In set theory, Silver machines are devices used for bypassing the use of fine structure in proofs of statements holding in L. They were invented by set theorist Jack Silver as a means of proving global square holds in the constructible universe.
Preliminaries
An ordinal  is *definable from a class of ordinals X if and only if there is a formula
is *definable from a class of ordinals X if and only if there is a formula 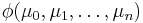 and
and 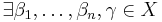 such that
such that  is the unique ordinal for which
is the unique ordinal for which 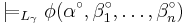 where for all
where for all  we define
we define 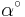 to be the name for
to be the name for  within
within 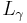 .
.
A structure 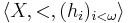 is eligible if and only if:
is eligible if and only if:
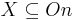 .
.- < is the ordering on On restricted to X.
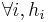 is a partial function from
is a partial function from 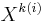 to X, for some integer k(i).
to X, for some integer k(i).
If 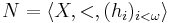 is an eligible structure then
is an eligible structure then 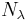 is defined to be as before but with all occurrences of X replaced with
is defined to be as before but with all occurrences of X replaced with  .
.
Let 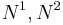 be two eligible structures which have the same function k. Then we say
be two eligible structures which have the same function k. Then we say 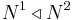 if
if 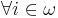 and
and 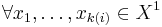 we have:
we have:
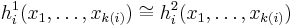
Silver machine
A Silver machine is an eligible structure of the form 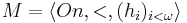 which satisfies the following conditions:
which satisfies the following conditions:
Condensation principle. If 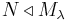 then there is an
then there is an  such that
such that 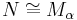 .
.
Finiteness principle. For each  there is a finite set
there is a finite set 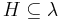 such that for any set
such that for any set 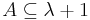 we have
we have
Skolem property. If  is *definable from the set
is *definable from the set 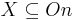 , then
, then ![\alpha \in M[X]](/2012-wikipedia_en_all_nopic_01_2012/I/c2f7610c70863eab48c4d94c5a8fea1a.png) ; moreover there is an ordinal
; moreover there is an ordinal ![\lambda < [sup(X) \cup \alpha]^%2B](/2012-wikipedia_en_all_nopic_01_2012/I/7c157592563fe2fd2e2d7e1b9d775772.png) , uniformly
, uniformly 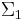 definable from
definable from 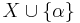 , such that
, such that ![\alpha \in M_\lambda[X]](/2012-wikipedia_en_all_nopic_01_2012/I/fbfb6b1cad6ada938c46b3a7f500dbd4.png) .
.
References
- Keith J Devlin (1984). "Chapter IX". Constructibility. ISBN 0-387-13258-9. - Please note that errors have been found in some results in this book concerning Kripke Platek set theory.
![M_{\lambda%2B1}[A] \subseteq M_\lambda[(A \cap \lambda) \cup H] \cup \{\lambda\}](/2012-wikipedia_en_all_nopic_01_2012/I/5ab0e9e853a1efb038dff40a79864acb.png)